และแล้วก็ผ่านมาได้ 2 อาทิตย์แล้วนะครับ หลังจากที่ผมได้เขียนเกี่ยวกับ Linear Regression ในบทความก่อนหน้าไป
ผมว่าเพื่อนๆก็คงอยากจะรู้แล้วว่า Model ที่เหลืออยู่ของ Supervised Learning เนี้ยคืออะไรบ้าง เพราะฉะนั้นผมว่า นี้ก็คงจะเป็นฤกษ์งามยามดีที่เราจะเปิด post ใหม่แล้วละครับ
หลักจากที่ Blog ที่แล้วเราได้เรียนรู้เกี่ยวกับ Linear Regression ทั้ง Simple และ Complex ไปแล้ว วันนี้เรามาดูอีกเทคนิคที่นิยมทำเพื่อแยกประเภท หรือแบ่งออกเป็น Classes อย่าง Classification กันดีกว่าครับ
คุณเคยมีประสบการณ์ที่ต้องเดาหรือเลือกคำตอบ yes/no ใช่/ไม่ใช่ ไหมครับ หรือ ในตอนที่คุณรู้สึกอยากจะเปลี่ยนโปรโทรศัพท์ อยู่ๆค่ายมือถือก็เลือกโทรมาหาคุณเพื่อขายโปรโมชั่น คุณเคยสงสัยไหมว่าพวกเขารู้ได้อย่างไร ติดกล้องในห้องเราหรือเปล่านะ หรือบางทีคุณอาจจะคิดว่ามันก็แค่ บังเอิญ ?
พูดกันตามตรงข้อมูลเหล่านี้มันมีเบื้องลึกเบื้องหลังมากกว่านั้น และวันนี้ผมก็มีคำตอบมาให้พวกคุณได้คลายความสงสัยเสียที เมื่อพร้อมแล้วไปลุยกั๊นน
Table of Content
- What is Classification ?
- General Classification Algorithms
- Let’s Implement them (Python Coding)
- Imbalance Dataset
- Evaluation
- Conclusion
What is Classification
Classification เป็นหนึ่งในประเภท Algorithms ภายใต้วิธีการสอนแบบ Supervised Learning โดยมีเป้าที่จะจัดหมวดหมู่ข้อมูล (Categorization) หรือ การทำนายกลุ่ม (Class Prediction) ที่เราต้องการทำนายค่า โดยใส่ค่าบางอย่างเข้าไปเช่น X (ข้อมูลดิบ) แล้วได้ค่า y (ประเภท) ออกมานั้นแหละคือ Classification Algorithm.
สำหรับ Classification เองก็สามารถแบ่งย่อยได้เป็นสองกลุ่มใหญ่ได้แก่
- Binary Classification: ประเภทที่ได้คำตอบออกมาสองค่า ก็คือ 0 กับ 1 เช่น
Yes/NoSpam/ Not Spam,Disease/ No Disease - Multi-class Classification: ประเภทที่จัดกลุ่มข้อมูลออกเป็นมากกว่าแค่ 2 ค่า ยกตัวอย่างเช่น ประเภทของสิ่งมีชีวิต แบ่งตาม Specie หรือ ตาม Phylum พวกผลไม้ และ พวกประเภทตัวเลขต่างๆ
ก่อนที่เราจะไปดูว่าใน Classification มี Algorithm อะไรบ้าง เรามาดูนิยามคำศัพท์กันก่อน เพื่อที่เมื่อเข้า Session ถัดไปแล้วก็จะได้ไม่งงกันครับ

| คำศัพท์ | ความหมาย |
|---|---|
| Features/Independent Variables (ตัวแปรอิสระ) | คุณลักษณะต่างๆ ของข้อมูล ที่เราใช้เป็น ‘วัตถุดิบ’ ในการทำนาย เช่น อายุ, เพศ, จำนวนบุหรี่ที่สูบ (X) |
| Labels/Classes/Dependent Variables (ตัวแปรตาม) | ตัวแปรที่จะได้รับผลกระทบหากเราเปลี่ยนแปลงวัตถุดิบ y (ผลลัพธ์ที่เราต้องการทำนาย, ประเภท) |
| Training Data, Testing Data | ข้อมูลสำหรับ ‘สอน’ ให้โมเดลฉลาด และ ข้อมูลสำหรับ ‘ทดสอบ’ ว่าโมเดลที่เราสอนมานั้นเก่งแค่ไหน |
| Algorithm | สูตร หรือ กระบวนการ’ที่ใช้ในการเรียนรู้จากข้อมูลเพื่อสร้าง ‘โมเดล’ ขึ้นมา |
| Prediction | การทำนาย หรือการคาดคะเน |
| Churn Analysis | การทำนายลักษณะของลูกค้าที่มีแนวโน้มกำลังจะยกเลิกบริการหรือมีแนวโน้มจะไม่กลับมาซื้อสินค้าหรือบริการซ้ำอีก |
General Classification Algorithm
สำหรับการทำ Classification Supervised Learning แล้ว ในปัจจุบันมีอัลกอริทึมหลายแบบมาก ซึ่งแต่ละอัลกอริทึมก็มีจุดแข็งและจุดอ่อนของตัวเองแตกต่างกันออกไป โดยขึ้นอยู่กับวิธีใช้ของผู้ใช้งาน ทั้งนี้เราก็ควรจะรู้จักแต่ละตัวไว้บ้างเพื่อให้เราไม่ติดกับดับ No Free Lunch ตามที่เราได้กล่าวไปในบทความก่อนหน้านี้
มาเริ่มกันที่ตัวแรกและถือว่าเป็นตัวพื้นฐานสุดเลยอย่าง Logistic Regression
ทุกคนอาจจะสงสัยทำไมชื่อมันคล้ายกับตัวก่อนหน้าอย่าง Linear Regression เลย สองอัลกอริทึมนี้เป็นอะไรกันหรือเปล่า ? คำตอบก็คือ ใช่ครับ! สองตัวนี้มีความเกี่ยวข้องกันนั้นก็คือใช้พื้นฐานทางสมการทางคณิตศาสตร์เหมือนกัน นั้นคือสมการเส้นตรง แต่วัตถุประสงค์แตกต่างกันอย่างสิ้นเชิงเลยครับ
Linear Regression: ใช้ทำนายค่าตัวเลขที่ต่อเนื่องไปเรื่อยๆ (เช่น ราคาบ้าน, ยอดขาย)
Logistic Regression: ใช้ทำนายความน่าจะเป็นเพื่อ “จัดกลุ่ม” หรือ “ตัดสินใจ” ว่าข้อมูลนั้นควรเป็นคลาสไหน (เช่น ใช่/ไม่ใช่, ป่วย/ไม่ป่วย, สแปม/ไม่ใช่สแปม)
Logistic Regression
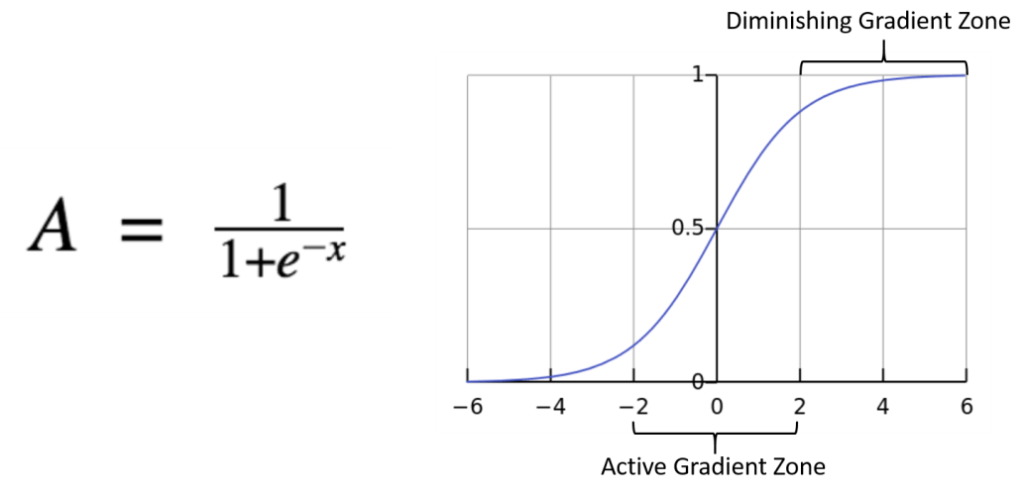
แต่มีจุดต่างตรงที่ Logistic Regression จะนำ สมการเส้นตรงไปจำกัดขอบเขต ด้วย Sigmoid Function หรือ Logistic Function เพื่อให้ผลลัพธ์อยู่ในช่วง 0 ถึง 1 เสมอ
เมื่อข้อมูลเราอยู่ระหว่าง 0 ถึง 1 นั้นหมายความว่ายิ่งข้อมูลมีค่าเข้าใกล้ 1 มากเท่าไหร่นั้นแปลว่าข้อมูลเหล่านั้นก็จะสามารถติดอยู่ในคลาส ใช่ หรือ 1 นั้นเอง
ในสมการของ Sigmoid Function เพื่อนๆอาจจะสงสัยว่าตัว e คืออะไร ตัว e เป็นค่าคงที่ในวิชาคณิตศาสตร์ที่เรียกว่า Euler Value ซึ่งจะมีค่าเท่ากับ 2.71828 นั้นเอง
ข้อดี (Pros) 👍
- เข้าใจง่าย สามารถเขียนเป็นรูปสมการและอธิบายได้อย่างเข้าใจ
- ผลลัพธ์ตีความได้ (แปลงออกมาเป็นความน่าจะเป็นได้)
- ประสิทธิภาพที่ดีและสามารถใช้เป็น Baseline ของการทำ Binary Classification
ข้อเสีย (Cons) 👎
- อ่อนไหวต่อ Outliers: ข้อมูลที่โดดไปจากกลุ่มมากๆ อาจส่งผลกระทบต่อการลากเส้นตัดสินใจได้
- หากข้อมูลที่มี Features เยอะอาจจะทำได้อย่างไม่เต็มประสิทธิภาพ
def logistic_regression_model(df_X_scaled, y):
X_trained, X_test, y_trained, y_test = train_test_split(df_X_scaled, y, test_size = 0.2, train_size=0.8, random_state = 42)
lr = LogisticRegression(random_state = 42, max_iter= 1000)
lr.fit(X_trained, y_trained)
evaluation_model('Logistic Regression',lr,y_test, X_test)
return
Decision Tree

อัลกอริทึมที่สองสำหรับการทำ Classification นั้นคือ Decision Tree (ต้นไม้ตัดสินใจ) ครับ อันที่จริงแล้วโมเดลนี้สามารถใช้ร่วมกันระหว่าง Regression หรือ Classification ก็ได้ โดยมีวัตถุประสงค์เพื่อที่จะทำนายค่า y โดยอ้างอิงวิธีที่มนุษย์ใช้ในการตัดสินใจ โดยแบ่งการตัดสินใจเป็นเงื่อนไขเล็กๆ เช่น สมมติเราจะซื้อของ 1 ชิ้น สมองก็จะค่อยๆแบ่งออกเป็นคำถามเล็กเพื่อตอบคำถามหลัก (ซื้อหรือไม่ซื้อ) เป็น สเปคดีไหม ? สีใช่ที่ชอบไหม ? ซื้อมาเอาไปทำไร ? คุ้มไหม ? เป็นต้น
ข้อดี
- ง่ายต่อการเข้าใจ สามารถสร้างเป็นกราฟได้
- เตรียม data ง่าย บางครั้งแทบไม่ต้องใส่ข้อมูลในช่วงที่หายไป หรือเอา NULL ออกก็ได้ (แต่เราควรทำให้ข้อมูลสะอาดที่สุดนะครับเพื่อลดการผิดพลาดของการนำไปใช้)
- ทำงานได้ดีมากกับข้อมูลที่มีความหลากหลายในด้าน features
- ค่า Cost สำหรับการรัน Model. จะเป็น log(n) สำหรับจำนวน data ที่ใช้สอน โมเดล ส่งผลให้สามารถทดสอบกับข้อมูลจำนวนมากได้
ข้อเสีย
- การทำนายของ Decision Tree จะไม่ได้อยู่ในลักษณะที่เป็นตัวเลข ต่อเนื่อง Continuous number แต่จะเป็นค่าคงที่เฉพาะเอง ซึ่งนั้นหมายความว่าตัวโมเดลไม่เหมาะที่จะใช้ทำนายข้อมูลที่ต้องการดูแนวโน้มหรือ เทรนด์ (Extrapolation)
- ด้วยความที่บางครั้ง Decision Tree ชอบสร้าง แขนงการตัดสินใจที่ซับซ้อนจนมากเกินไป อาจเกิดเหตุการณ์ Overfitting ได้ ซึ่งเราอาจจะเปลี่ยนไปใช้ Random Forest แทนเพื่อแก้ปัญหานี้
- หากข้อมูลมี Outlier ผิดปกติเยอะอาจส่งผลต่อโครงสร้างของ Decision Tree นำไปสู่การทำนายที่ให้ผลลัพธ์ที่ผิดปกติได้
def decision_tree_model(df_X_scaled, y):
X_trained, X_test, y_trained, y_test = train_test_split(df_X_scaled, y, test_size = 0.2, train_size=0.8, random_state = 42)
clf = DecisionTreeClassifier(random_state=42)
clf.fit(X_trained,y_trained)
evaluation_model('Decision Tree',clf, y_test, X_test)
return
Random Forest
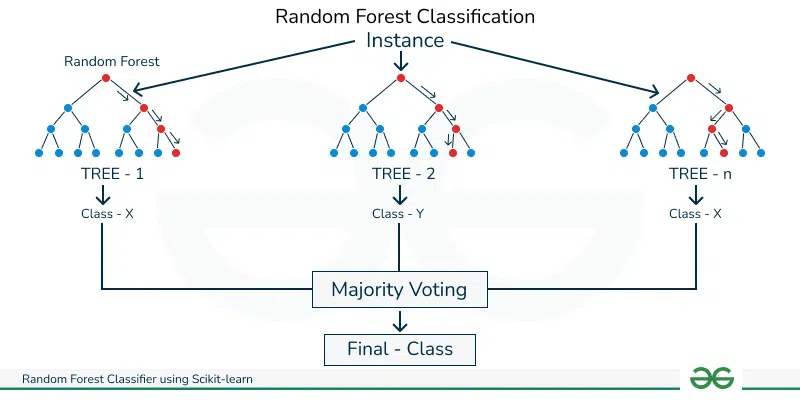
อัลกอริทึม ถัดไปที่เป็นการต่อยอดจาก Decision Tree นั้นคือ Random Forest อัลกอรึทึมนี้เกิดจากการที่เรานำผลลัพธ์มากมายจาก Decision Trees หลายๆอัน และสรุปออกมาเป็นผลลัพธ์เดียว
โดย Random Forest ถือว่าเป็นส่วนหนึ่งของ Ensumble Learning หรือ กลุ่มอัลกอริทึมที่เกิดจากการเทรนอัลกอริทึมเดิมซ้ำๆ หลายรอบ บนข้อมูลชุดเดียวกันจนได้ผลลัพธ์ โดยในแต่ละครั้งก็จะจัดสัดสวนข้อมูลที่ใช้เทรนไม่เท่ากันด้วย
โมลเดลนี้สามารถนำไปใช้ได้ทั้งใน Regression หรือ Classification ก็ได้
ข้อดี
- ด้วยความที่ข้อมูลถูกเทรนซ้ำๆ ด้วยการแบ่งสัดส่วนที่ไม่เหมือนกัน (Bootstrap Aggregating (Bagging)) ส่งผลให้ความแม่นยำนั้นสูงเช่นกัน จินตนการเหมือนกับที่เราถามคำถามเดียวกันกับฝูงชน แล้วเราค่อยสรุปออกมาเป็นคำตอบเดียวจากหลายๆคำตอบนั้นเอง
- จากที่ได้กล่าวใน โมเดลที่แล้วก็คือช่วยป้องกันการเกิด Overfitting
- มีความหยืดหยุ่นมากในการทำ Hyper-parameters Tuning
ข้อเสีย
- ความยากในการตีความ (Interpretability) เพราะต้นไม้แต่ละค้นนั้นก็จะมีการเลือกใช้ Features ไม่เหมือนกัน (Feature Randomness)
- มีต้นทุนสูงเนื่องจากว่าต้องผ่านการคำนวณหลายครั้ง
def random_forest_model(df_X_scaled, y):
X_trained, X_test, y_trained, y_test = train_test_split(df_X_scaled, y, test_size = 0.2, train_size=0.8, random_state = 42)
rfc = RandomForestClassifier(random_state = 42)
rfc.fit(X_trained, y_trained)
evaluation_model('Random Forest',rfc, y_test, X_test)
return
K Nearest Neighbours
อีกหนึ่งโมเดลที่เป็นที่นิยมและใช้งานง่ายมากๆ นั้นคือ knn หรือ K Nearest Neighbour โมเดลที่จะหาทำนายค่า จะดึงข้อมูลที่ใกล้เคียงตัวมันเองที่สุด K ตัว แล้วก็ค่อยดูว่าจาก K ตัวเป็น Class อะไรบ้าง
KNN สามารถประยุกต์ใช้ได้ทั้งใน Classification หรือ Regression ก็ได้โดยที่
- เราจะหาผลโหวตที่มากที่สุด หากเราทำ Classification
- เราจะหาค่าเฉลี่ยของ K ทุกตัวหากเราทำ Regression เพื่อ Predict บางอย่าง
ข้อดี
- Implement ได้ง่าย และ Train ง่าย เพราะตัวอัลกอริทึมเองนั้นจำข้อมูลอย่างเดียวในช่วงที่ Train ข้อมูล ( Lazy Learner )
- ใช้กับ Test Data หรือ Data ใหม่ที่โมเดลไม่เคยเห็นได้ดี
ข้อเสีย
- อัลกอริทึมนี้ sensitive มาก ถ้าเจอข้อมูลที่ Outlier เยอะๆ Missing Value, หรือ NaN ละก็เตรียมตัวระเบิดได้เลย
- KNN ทำงานได้ช้ามากเมื่อมีข้อมูลเยอะ (Poor Scalability) เพราะทุกครั้งที่ ทำการทำนายมันจะต้องคำนวณระยะทุกๆจุด ใช่ครับมีล้านจุดก็ทำนายล้านที ต่างจากเพื่อนๆของมันที่ Train มาก่อนแล้ว
- KNN จะทำได้ไม่ดีนักหากข้อมูลของเรามี Features เยอะมากๆ คุณลองคิดดูสิถ้าสมมติว่าข้อมูลมี 50 features มันก็จะดูห่างกันมาก ดูไม่ได้ใกล้เคียงกับใครเลย
- การกำหนด K เหมือนจะง่าย แต่จริงๆ แล้วอาจจะให้ค่าที่ต่างกันหากไม่ระวัง
def knn_model(df_X_scaled, y):
X_trained, X_test, y_trained, y_test = train_test_split(df_X_scaled, y, test_size = 0.2, train_size=0.8, random_state = 42)
knn = KNeighborsClassifier()
knn.fit(X_trained,y_trained)
evaluation_model('K-nearest neighbourhood', knn ,y_test, X_test)
return
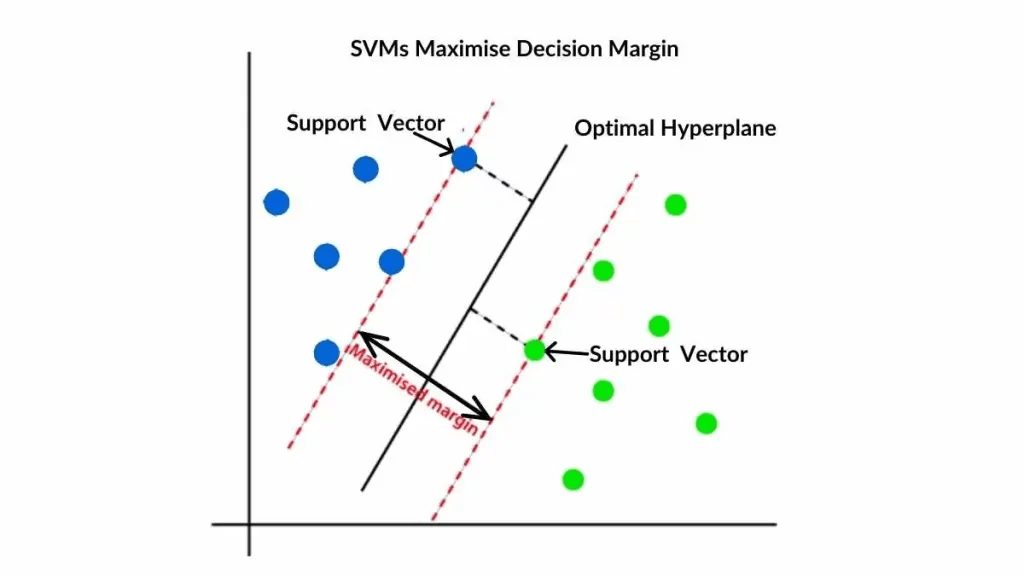
Support Vector Machines
สำหรับอัลกอริทึมสุดท้ายสำหรับบทความนี้ นั้นคือ อัลกอริทึมที่มีชื่อว่า SVM หรือ Support Vector Machines ซึ่งเป็นอัลกอที่มีความยืดหยุ่นมาก เมื่อข้อมูลมีความซับซ้อน หลาย Feature แต่จำนวน data ดันน้อย
หลักการของ SVM คือการพยายามสร้าง ‘ถนน’ ที่กว้างที่สุดเท่าที่จะเป็นไปได้เพื่อแบ่งกลุ่มข้อมูลออกจากกัน โดยเส้นขอบถนนทั้งสองข้างก็คือ Support Vectors นั่นเอง
ข้อดี
- มีความยืดหยุ่นมาก
- ทำงานได้ดีกับ ข้อมูลที่มี Dimensions เยอะแต่จำนวน data น้อย
- สามารถจัดการกับข้อมูลที่ไม่เป็นเชิงเส้นได้ดีเยี่ยมด้วยเทคนิค Kernel Trick ถามว่า Kernel Trick คืออะไรมันก็คือการที่คุณพยายามจะแก้ปัญหาที่ไม่สามารถลาก เส้นตรงเส้นเดียวเพื่อแบ่งของได้ ยกตัวอย่างเช่น สมมติมี ถั่วสีน้ำเงินกับ สีเขียวอยู่บนโต๊ะปนๆกันอยู่ ถ้ามองก็จะเห็นเป็น 2 มิติใช่ไหมครับแยกไม่ได้เลย การใช้ Kernel Trick ก็เหมือนการที่คุณทุบใต้โต๊ะแล้วถั่วก็ลอยขึ้น อยู่ในมุมมอง 3 มิติ ส่งผลให้คุณสามารถใช้กระดาษ ( Hyperplane ) เพื่อสอดเข้าไประหว่างกลางเพื่อทำการแบ่ง นั้นแหละคือ Kernel Trick
ข้อเสีย
- อาจทำงานได้ไม่ดีกับชุดข้อมูลขนาดใหญ่มาก ๆ (เนื่องจากการคำนวณที่ซับซ้อน) หรืออาจต้องใช้เวลาในการปรับแต่ง Kernel ที่เหมาะสมเพื่อจัดการกับข้อมูลที่ไม่เป็นเชิงเส้น
def svc_model(df_X_scaled, y):
X_trained, X_test, y_trained, y_test = train_test_split(df_X_scaled, y, test_size = 0.2, train_size=0.8, random_state = 42)
svc = SVC(random_state = 42, probability=True)
svc.fit(X_trained, y_trained)
evaluation_model('Support Vector Machines', svc,y_test, X_test)
return
หลังจากที่เราได้เรียนรู้อัลกอริทึมต่างๆ ขั้นตอนตอไปก็คือลองลงมือ Implement จริงดู ไปกันเล๊ยย
Let’s Implement them w8 Python Code
สำหรับรอบนี้ผมเลือกใช้ ข้อมูลชุดที่มีชื่อว่า framingham.csv สำหรับการ Train นะครับเป็นข้อมูลที่เกี่ยวกับคนไข้ที่ป่วยและมีแนวโน้มจะเป็นโรคหลอดเลือดหัวใจในระยะ 10 ปี หรือไม่
ข้อมูลนี้จะประกอบไปด้วย 4,240 records และ 16 Columns เรามาลองดูแต่ละ Column กันดีกว่าครับ
| คำศัพท์ | ความหมาย |
|---|---|
| male | ระบุเพศของผู้ป่วย ชาย 1 หญิง 0 |
| age | อายุของผู้ป่วย |
| education | ระดับการศึกษามี (1-4) |
| currentSmoker | สถานะว่าสูบบุหรี่อยู่หรือไม่ 0 คือไม่สูบและ 1 คือยังสูบ |
| cigsPerDay | จำนวนบุหรี่ที่สูบในแต่ละวัน |
| BPMeds | ระบุว่าผู้ป่วยรับประทานยาลดความดันโลหิต (1) หรือไม่ (0) |
| prevalentStroke | ระบุว่าผู้ป่วยมีประวัติเป็น Stroke หรือไม่ 1 คือเป็น 0 คือไม่ |
| prevalentHyp | ระบุว่าผู้ป่วยมีประวัติเป็น Hypertension |
| diabetes | ระบุว่าผู้ป่วยมีประวัติเป็นโรคเบาหวาน (1) หรือ ไม่ (0) |
| totChol | ปริมาณโคเลสเตอรอลของผู้ปวย |
| sysBP | ความดันโลหิตซิสโตลิกของผู้ป่วย |
| BMI | BMI ของผู้ป่วย |
| heartRate | อัตราการเต้นของหัวใจผู้ป่วย |
| glucose | ระดับน้ำตาลกลูโคสของผู้ป่วย |
| TenYearCHD | ระบุผลลัพธ์ว่าผู้ป่วยมีแนวโน้มจะเป็นโรคหลอดเลือดหัวใจในระยะ 10 ปี หรือไม่ |
| diaBP | ความดันโลหิตไดแอสโตลิกของผู้ป่วย |
หลังจากรู้แล้วว่าแต่ละ Columns คือค่าอะไรเรามาลุยกันเลยดีกว่าครับทุกคน โดยเป้าหมายของเราก็คือ การสร้างโมเดลเพื่อทำนายความเสี่ยงของการเกิดโรคหลอดเลือดหัวใจในอีก 10 ปีข้างหน้าให้ได้ ป่ะลุยกัน 🔥
Preprocessing
ขั้นแรกเราก็ต้องโหลด dataset กันก่อนด้วย Library Pandas
df = pd.read_csv('framingham.csv', decimal=',', sep=',', header =0)
หลังจากนั้นก็ทำการ drop Null Value ออกด้วย dropna()
หมายเหตุ
สำหรับบทความนี้เราจะ drop ข้อมูลที่เป็น Null ออกไปเพื่อความกระชับของเนื้อหา แต่ในโลกของความเป็นจริงนั้น เราไม่ควรที่จะทำเช่นนั้น เพราะมีโอกาสทำให้ผลลัพธ์ของโมเดลเพี้ยนได้
วิธีการที่ดีกว่าในกรณีเช่นนี้ ก็คือการที่เราแทนค่าลงไปด้วย Mean/Meadian Imputation จะช่วยให้โมเดลทำงานได้ดีกว่าครับ
df.dropna(inplace=True)
ลองตรวจว่าข้อมูลผลลัพธ์ผู้ป่วยกระจายตัวแบบใด
print(df['TenYearCHD'].value_counts(normalize=True))
ทำไมต้องใส่
normalize= True ?
เพราะว่า โดยปกติแล้ว value_counts จะคืนค่าที่มีมากที่สุดใน columnที่เราเลือกก่อนเสมอและอยู่ในลักษณะของความถี่ธรรมดา อย่างไรก็ตาม หากเราต้องการจะเปรียบเทียบว่าข้อมูลมันเอียงไปทางใดทางหนึ่งหรือไม่นั้น (ข้อมูลไม่ใช่กระจายตัวสม่ำเสมอ) การใส่ normalize = True จะแปลงตัวเลขให้เป็นความถี่สัมพัทธ์ มีค่า [0,1] แทน ซึ่งง่ายต่อการตรวจสอบและทำความเข้าใจ
เดี๋ยวเราจะกลับมาดูค่านี้กันไหมนะครับ ไปดูตรงอื่นๆกันก่อน
เนื่องจาก .csv ที่ผมโหลดมา ดันให้ sysBP เป็น object type ซะงั้นผมก็เลยต้องแปลงค่าเสียก่อน
df['sysBP'] = pd.to_numeric(df['sysBP'])
หลังจากนั้นเราก็มาทำการ clean outlier กันต่อครับ โดยผมเลือกใช้วิธี เช็คด้วย IQR (Inter Quartile Range) และแทนค่าค่าที่เกินขอบเขตแทนที่จะลบออกครับ เพราะ Dataset จะหายไปราวๆ 15% หรือ 800 rows เลยทีเดียวถ้าเราไม่เก็บค่าพวกนี้ไว้ ซึ่งอาจส่งผลต่อ metrics ต่างๆได้
features = ['male', 'age', 'cigsPerDay' , 'totChol', 'sysBP', 'glucose' ]
y = df['TenYearCHD']
X_processed = df[features].copy()
for col in features:
X_processed[col] = cap_outliers_iqr(X_processed[col])
def cap_outliers_iqr(df_column):
q1 = df_column.quantile(0.25)
q3 = df_column.quantile(0.75)
IQR = q3 - q1
lower_bound = q1 - 1.5*IQR
higher_bound = q3+ 1.5*IQR
capped_column = np.where(df_column < lower_bound, lower_bound, df_column)
capped_column = np.where(capped_column > higher_bound, higher_bound, capped_column)
return pd.Series(capped_column, index = df_column.index)
หลังจากนั้นเราก็มาทำการแปลง scale ข้อมูลด้วย StandardScaler เพื่อให้ข้อมูลอยู่บนบรรทัดฐานเดียวกันป้องกันการทำนายผิดพลาด
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X_processed)
f_X_scaled = pd.DataFrame(X_scaled, columns =X_processed.columns)
StandardScaler เป็นหนึ่งใน feature scaling เทคนิคที่จะทำให้ข้อมูลของเรามีค่าเฉลี่ย เป็น 0 และ มีค่าการกระจายตัวของข้อมูลเป็น 1 ตามหลักการกระจายตัวปกติ วิธีนี้เป็นวิธีที่เหมาะต่ออัลกอริทึมอย่าง SVM และ Logistic Regression เพราะทั้งคู่ต้องการให้ข้อมูลอยู่ในลักษณะกระจายตัวปกติ
ถึงแม้ว่าการทำ Scaling จะไม่ส่งผลโดยตรงต่อประสิทธิภาพของโมเดลประเภท Tree-based อย่าง Decision Tree หรือ Random Forest แต่การทำไว้ก็ถือเป็น Good Practice เมื่อเราต้องการทดลองหลายๆ โมเดลพร้อมกันครับ
และสุดท้าย แบ่งข้อมูลเป็นสัดส่วน
X_trained, X_test, y_trained, y_test = train_test_split(df_X_scaled, y, test_size = 0.2, train_size=0.8, random_state = 42)
ในอนาคตเราจะมีเจาะลึกวิธีการแบ่งข้อมูลด้วยเทคนิคอื่นๆกันครับ ตอนนี้เราใช้ Train Test Split ไปก่อน
Train Models
models = {
'Logistic Regression': LogisticRegression(random_state=42, max_iter=1000),
'Decision Tree': DecisionTreeClassifier(random_state=42),
'Random Forest': RandomForestClassifier(random_state=42),
'K-Nearest Neighbors': KNeighborsClassifier(),
'Support Vector Machine': SVC(random_state=42, probability=True)
}
for model_name, model in models.items():
model.fit(X_trained, y_trained)
อย่าลืมใส่ probability=True เพื่อให้เราสามารถอ่านค่า AUC ได้
Score
เมื่อเรา Train เสร็จแล้วก็ถึงเวลาวัดผลแล้วละ
def evaluation_model(model_name, model,y_test,X_test):
y_pred = model.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
print(f'Model : {model_name}')
print(cm)
print(f'Accuracy Score: {accuracy_score(y_test, y_pred)}')
print(f'Precision Score: {precision_score(y_test, y_pred)}')
print(f'Recall Score: {recall_score(y_test,y_pred)}')
print(f'F1 Score: {f1_score(y_test, y_pred)}')
print(classification_report(y_test,y_pred,target_names=['NO CHD (0)', 'CHF (1)']))
if hasattr(model, 'predict_proba'):
y_pred_proba = model.predict_proba(X_test)[:, 1] # Probability of the positive class (1)
roc_auc = roc_auc_score(y_test, y_pred_proba)
print(f"ROC AUC Score: {roc_auc:.4f}")
else:
print("ROC AUC Score: Not available (model does not provide probabilities directly).")
print(f"{'='*50}\n")
อะอะ ก่อนไปดูผลลัพธ์เรามาทำความรู้จัก Metrics ต่างกันก่อนดีกว่า
เริ่มกันที่ตัวแรกเลย Accuracy
Accuracy
Accuracy คือ metric ที่ใช้งานง่ายที่สุด ตามชื่่เลยครับว่า ความแม่นยำ บอกว่าโมเดลเราทำนายถูกทั้งหมดกี่ % จากตาราง Confusion Matrix เราสามารถคำนวณได้ด้วยสูตรข้างล่างนี้
ถ้าแบบทางการหน่อย เราจะเขียนสูตรว่า accuracy = (TP + TN)/ N โดยค่า accuracy จะมีค่าอยู่ระหว่าง 0-1 ยิ่งเข้าใกล้ 1 แปลว่าโมเดลเราทำนายผลได้ดีมาก
Precision
จริงๆ อันนี้ก็แปลว่าความแม่นยำ เหมือนกัน แต่จะมีความหมายคนละแบบ นิยามของ Precision คือความน่าจะเป็นที่โมเดลทำนาย CHD คิดเป็นจากการทำนายถูกทั้งหมดกี่ % หรือก็คือ ถ้าชี้หน้าว่า คนๆนี้ป่วย โอกาสที่ป่วยก็คือ Precision% นั้นเอง
แทนค่าในสมการ precision = TP / (TP + FP)
Recall
นิยามของ Recall คือความน่าจะเป็นที่โมเดลสามารถตรวจจับ คนเป็น CHD จากจำนวน CHD ทั้งหมดใน ผลรวมคอลั่มแรกของ confusion matrix) สมมติในโรงพยาบาลมีคนไข้ 100 คน ถ้าตรวจพบแค่ 70 ก็คือมี ค่า Recal ที่ 70%
แทนค่าในสมการ recall = TP / (TP + FN)
F1-Score
F1-Score คือค่าเฉลี่ยแบบ harmonic mean ระหว่าง precision และ recall นักวิจัยสร้าง F1 ขึ้นมาเพื่อเป็น single metric ที่วัดความสามารถของโมเดล (ไม่ต้องเลือกระหว่าง precision, recall เพราะเฉลี่ยให้แล้ว) เพราะตามความเป็นจริง Precision และ Recall จะสวนทางกัน เขาก็เลยคิด F1-Score เพื่อปิดจุดอ่อนนี้
ข้อควรระวัง
- การดูแต่ค่า Accuracy อย่างเดียวมีโอกาสอธิบายการทำนายผิดพลาดได้
- ในทางปฏิบัติเราจะดูค่า precision, recall, F1 ร่วมกับ accuracy เสมอ โดยเฉพาะอย่างยิ่งเวลาเจอกับปัญหา imbalanced classification i.e. y {0,1} มีสัดส่วนไม่เท่ากับ 50:50
AUC
AUC ย่อมาจาก “Area Under Curve” AUC มีค่าอยู่ระหว่าง 0-1 ยิ่งเข้าใกล้ 1 แปลว่าโมเดลทำนาย Y ได้ดี เป็นอีก 1 ใน metrics สำคัญมากๆในงาน Datascience
ด้านล่างคือผลลัพธ์ที่ได้ของแต่ละโมเดล
เอาละหลังจากรู้จัก Metrics ต่างๆละเรามาดูผลลัพธ์กันเล๊ยยย~~~
Model : Logistic Regression
[[605 5]
[117 5]]
Accuracy Score: 0.8333333333333334
Precision Score: 0.5
Recall Score: 0.040983606557377046
F1 Score: 0.07575757575757576
precision recall f1-score support
NO CHD (0) 0.84 0.99 0.91 610
CHF (1) 0.50 0.04 0.08 122
accuracy 0.83 732
macro avg 0.67 0.52 0.49 732
weighted avg 0.78 0.83 0.77 732
ROC AUC Score: 0.7078
==================================================
Model : Decision Tree
[[528 82]
[ 89 33]]
Accuracy Score: 0.7663934426229508
Precision Score: 0.28695652173913044
Recall Score: 0.27049180327868855
F1 Score: 0.27848101265822783
precision recall f1-score support
NO CHD (0) 0.86 0.87 0.86 610
CHF (1) 0.29 0.27 0.28 122
accuracy 0.77 732
macro avg 0.57 0.57 0.57 732
weighted avg 0.76 0.77 0.76 732
ROC AUC Score: 0.5680
==================================================
Model : Random Forest
[[600 10]
[110 12]]
Accuracy Score: 0.8360655737704918
Precision Score: 0.5454545454545454
Recall Score: 0.09836065573770492
F1 Score: 0.16666666666666666
precision recall f1-score support
NO CHD (0) 0.85 0.98 0.91 610
CHF (1) 0.55 0.10 0.17 122
accuracy 0.84 732
macro avg 0.70 0.54 0.54 732
weighted avg 0.80 0.84 0.79 732
ROC AUC Score: 0.6859
==================================================
Model : K-Nearest Neighbors
[[588 22]
[104 18]]
Accuracy Score: 0.8278688524590164
Precision Score: 0.45
Recall Score: 0.14754098360655737
F1 Score: 0.2222222222222222
precision recall f1-score support
NO CHD (0) 0.85 0.96 0.90 610
CHF (1) 0.45 0.15 0.22 122
accuracy 0.83 732
macro avg 0.65 0.56 0.56 732
weighted avg 0.78 0.83 0.79 732
ROC AUC Score: 0.6241
==================================================
Model : Support Vector Machine
[[610 0]
[119 3]]
Accuracy Score: 0.837431693989071
Precision Score: 1.0
Recall Score: 0.02459016393442623
F1 Score: 0.048
precision recall f1-score support
NO CHD (0) 0.84 1.00 0.91 610
CHF (1) 1.00 0.02 0.05 122
accuracy 0.84 732
macro avg 0.92 0.51 0.48 732
weighted avg 0.86 0.84 0.77 732
ROC AUC Score: 0.6525
==================================================
หลังจากที่เราได้ผลลัพธ์ของแต่ละโมเดลมาเรียบร้อยแล้ว ก่อนที่จะไปประเมินผลลัพธ์ของแต่ละโมเดลกัน เรามาทำความเข้าใจกันก่อนว่า ทำไมผมถึงทักว่าเราจะกลับมาดูตรง value_count กันครับ
Imbalanced Dataset
หากเราลองดูค่า Relative Frequency ของ dataset นี้
TenYearCHD
0 0.847648
1 0.152352
คุณเห็นอะไรไหมครับ ใช่ ข้อมูลของคนที่ไม่ได้ป่วยเป็นโรคหลอดเลือดหัวใจ คิดเป็น 85% ของข้อมูลนี้ นั้นแปลว่าถ้าผมแค่นั่งเดา 100 ครั้งว่า คนนี้ไม่เป็นโรคหลอดเลือดหัวใจ ผมก็เดาถูกตั้ง 85% เลยนะครับ
เพราะฉะนั้นการดูแต่ค่า Accuracy อย่างเดียวก็อาจจะไม่สามารถบอกได้ว่า โมเดลนี้เป็นโมเดลที่ให้ผลลัพธ์ที่ดีทีสุดแล้วหรือยังนั้นเอง
และในกรณีนี้เมื่อมี Class หนึ่งที่เยอะผิดปกติ โมเดลก็มีแนวโน้มที่จะเรียนรู้และเดาข้อมูลที่มีเยอะกว่าได้แม่นยำกว่าส่งผลให้โอกาสที่จะทายข้อมูลอีกด้านนั้นลดลง
อย่างในกรณีนี้คุณลองคิดดูสิว่าถ้าโมเดลทำนายว่าคนนี้ไม่ได้เป็นหรอกโรคหลอดเลือดหัวใจ แต่จริงๆแล้วเขาเป็น มันจะอันตรายถึงชีวิตเขาขนาดไหน เขาอาจะถึงขั้นเสียชีวิตเลยก็ได้นะครับ
ในบทความถัดๆไป เราจะมีดูกันว่าจะมีวิธีการแก้ปัญหาอย่างไรในกรณีที่ข้อมูลไม่เท่ากันแบบนี้อีก เพื่อลดความผิดพลาดของโมเดลในการทำนายผลกันนะครับ
Evaluation
เรามาเริ่มกันที่ Logistic Regression กันก่อน
| โมเดล Classification | Accuracy (ความแม่นยำรวม) | Precision (Class 1) | Recall (Class 1) | F1-Score (Class 1) | ROC AUC Score |
|---|---|---|---|---|---|
| Logistic Regression | 0.836 | 0.5 | 0.041 | 0.076 | 0.7078 |
| Decision Tree | 0.766 | 0.287 | 0.27 | 0.278 | 0.568 |
| Random Forest | 0.836 | 0.545 | 0.098 | 0.167 | 0.6859 |
| K-Nearest Neighbors | 0.828 | 0.45 | 0.148 | 0.222 | 0.6241 |
| Support Vector Machine (SVM) | 0.837 | 1 | 0.025 | 0.048 | 0.6525 |
จากตารางข้างต้นจะเห็นได้ว่า Model ที่มีค่า ROC AUC มากที่สุดนั้นคือ Logistic Regression รองลงมาเป้น Random Forest นั้นแปลว่าสามารถจำแนกผู้ป่วยกับไม่ป่วยได้ค่อนข้างดีในหลากหลายสถานการณ์ สำหรับ Logistic Regresssion
อย่างไรก็ตามด้วยค่า Recall ที่แปลว่าคุณเดาถูกกี่ครั้งจากคนที่ป่วยทั้งหมด ดันได้คะแนนสำหรับ Class 1 แค่ 0.04 นั้นแปลว่าถ้ามี 100 คน จะบอกว่าป่วยได้แค 4 คนซึ่งนี้มันต่ำมากๆ
แม้ว่า Decision Tree จะมีค่า Recall สูงที่สุดใน 5 โมเดล แต่ก็มีค่า Precision ที่ต่ำที่สุดในกลุ่มเช่นกันก็คือถ้าทายว่าป่วยไม่ป่วยดันทายถูกแค่ 28% เท่านั้นอง
สำหรับ Random Forest นั้นแม้ว่าค่า Accuracy กับ ค่า ROC AUC จะทำได้ดีแต่ดันไปตกม้าตายที่ค่า Recall ที่ได้แค่ 0.1 เหมือนจะดีกว่า Logistic แต่ก็ยังทำผลงานได้แย่อยู่ดี เกินกว่าจะนำออกไปใช้จริงได้
ในส่วนของ KNN โดยภาพรวมแล้วไม่ได้หวือหวา หรือเด่นไปกว่าโมเดลไหนเลยครับ
และสุดท้าย SVM ที่มีคะแนน Precision = 1 เลยทีเดียวแปลว่าเดาว่าเป็นกี่ครั้งก็คือถูกหมดแต่ว่า ดันมีค่า Recall แค่ 0.025 ก็คือ ถ้ามี 100 คนมันจะเดาถูกแค่ 3 คน แต่ทุกครั้งที่ทำนายคือถูกชัวร์ แต่มันก็ต่ำเกินไปแปลว่ามันมีโอกาสข้ามคนป่วยถึง 97 คนเลยทีเดียว
Conclusion
สรุปแล้วในภาพรวมเมื่อสรุปและประเมินผลที่ได้โมเดลที่น่าจะทำผลงานได้ดีที่สุดหากมีการนำไปใช้จริงก็จะเป็น Logistic Regression ด้วยคะแนน ROC AUC ที่มากที่สุดนั้นเอง อย่างไรก็ตามด้วยค่า AUC แค่ 0.7 หรือ 70% นั้นถือว่ายังไม่ดีพอ (ถ้าดีควรจะมีค่ามากกว่า 80%) ซึ่งเป็นปัญหาทีเกิดจากการที่ข้อมูลที่เรามีนั้นไม่ได้สมดุลระหว่างผู้ป่วยที่เป็นโรคหัวใจ หรือไม่เป็น
ด้วยผลดังกล่าว อาจส่งผลให้โมเดลของเราดูมีค่าความแม่นยำ (Accuracy) ที่สูงแต่กลับไม่สามารถนำไปใช้ประโยชน์ได้จริงหากหน้างานต้องการความละเอียดอ่อน ลองคิดดูสิครับถ้าเราเอาโมเดลนี้ไปใช้ แล้วมันดันข้ามคนป่วยจริงๆไป ผมว่ามันเป็นอะไรที่เรารับไม่ได้แน่ๆครับ
ดังนั้น ในบทความข้างหน้า หลังจากที่เขียน Main Serie หมดแล้ว ผู้เขียนจะมานำเสนอวิธีการและประยุกต์ใช้เทคนิคต่างๆเพื่อจัดการกับปัญหาเหล่านี้
เพื่อให้โมเดลของเราไม่เพียงแค่ทำนายได้แม่นยำในภาพรวม แต่ยังสามารถตรวจจับ Class สำคัญได้อย่างมีประสิทธิภาพมากยิ่งขึ้น!”